چگونه کتابخوان تر شویم؟
سالهاست که هر وقت به من میگویند چه توصیه هایی برای پیشرفت بیشتر و بهتر داری، من کتاب خواندن را توصیه میکنم. اخیراً بعضی دوستانم میگویند که ما میخواهیم، اما به هزار و یک دلیل نمیشود. به عنوان آدمی که پانزده سال اخیر متوسط روزانه ۷۰ صفحه کتاب را خوانده ام، سعی کردم چند نکته مهم در این زمینه را اینجا بنویسم:
اول اینکه) تلاش کنید غیر از فارسی زبان دومی را هم بدانید. طبیعی است دست شما در پیدا کردن کتاب مناسب بازتر میشود. شاید برای کسانی که کار فنی میکنند یا فلسفه میخوانند، زبان آلمانی، برای مدیریت و اقتصاد زبان انگلیسی و برای شیفتگان ادبیات زبان فرانسه گزینه های جذابی باشند. البته من در این مورد صاحب نظر نیستم و این حرف کاملاً سلیقه شخصی من است. دانستن زبان دوم حتی میزان درک زبان اول را نیز بالا می برد. این نکته ای است که سالهاست در روانشناسی اثبات شده است.
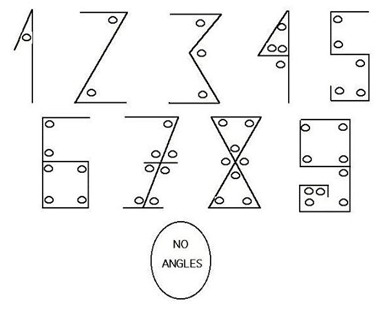



 آموزش مفاهیم ریاضیات
آموزش مفاهیم ریاضیات